QTCAD (Quantum-Technology Computer-Aided Design) is a finite-element (FEM) simulator used to predict the performance of solid-state spin-qubit devices. It calculates the envelope functions and energy levels of electrons or holes confined in nanostructures using K.P theory.
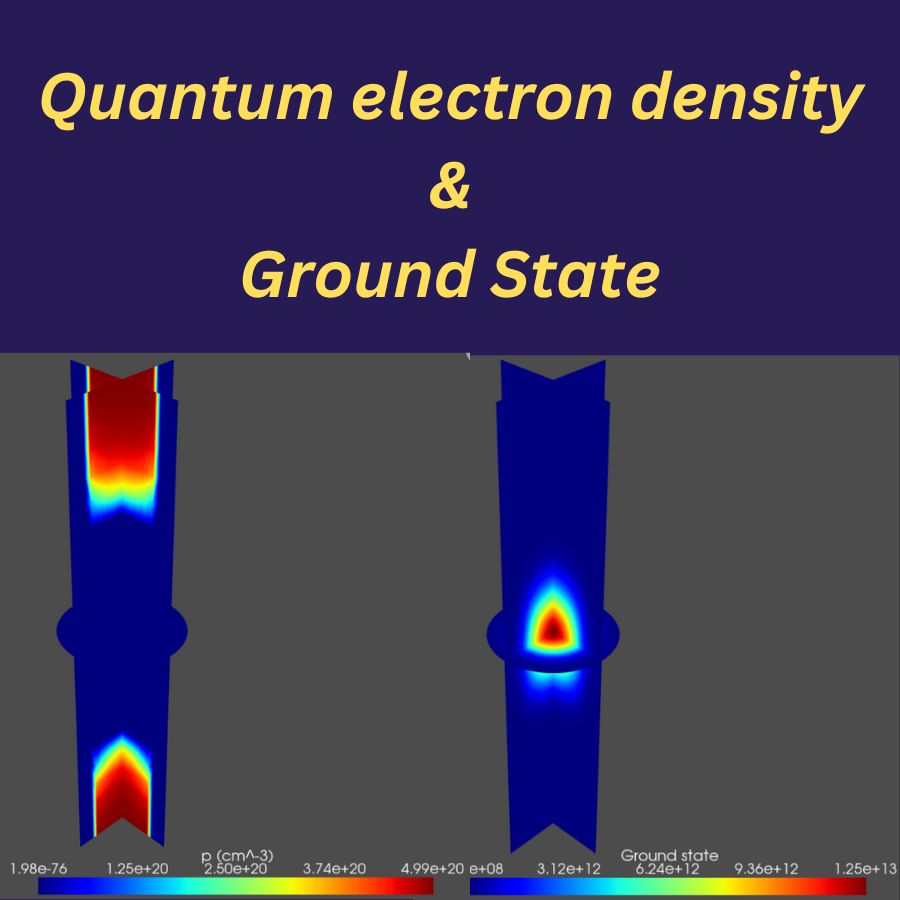
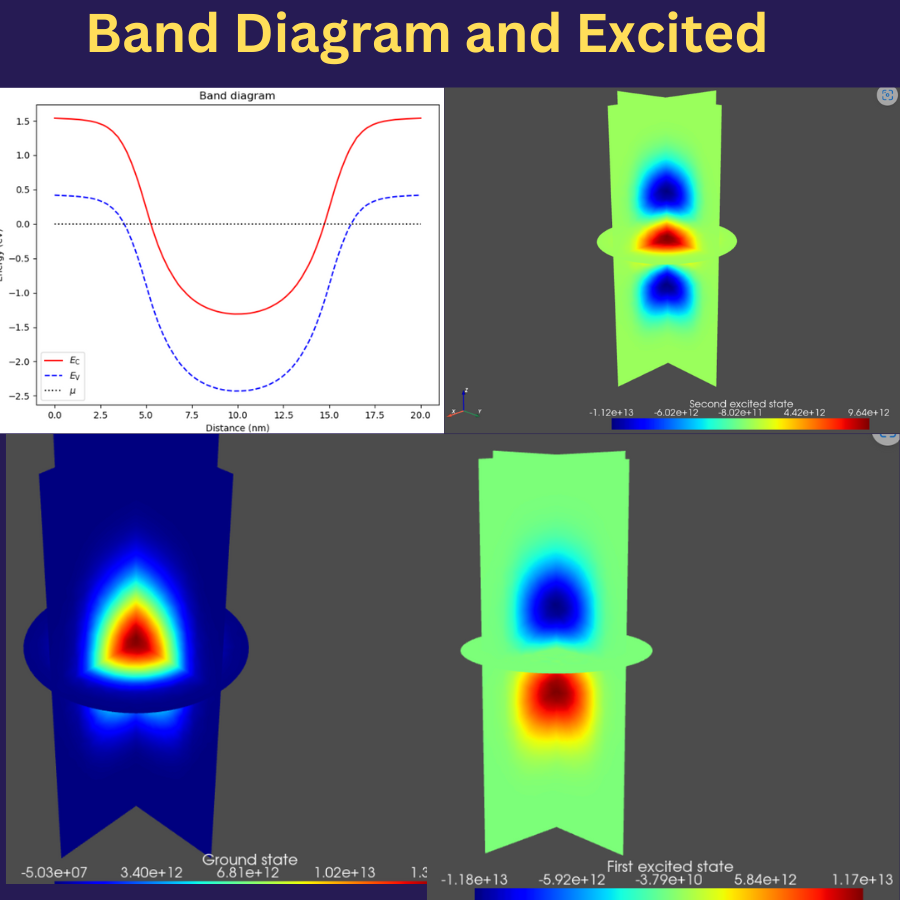
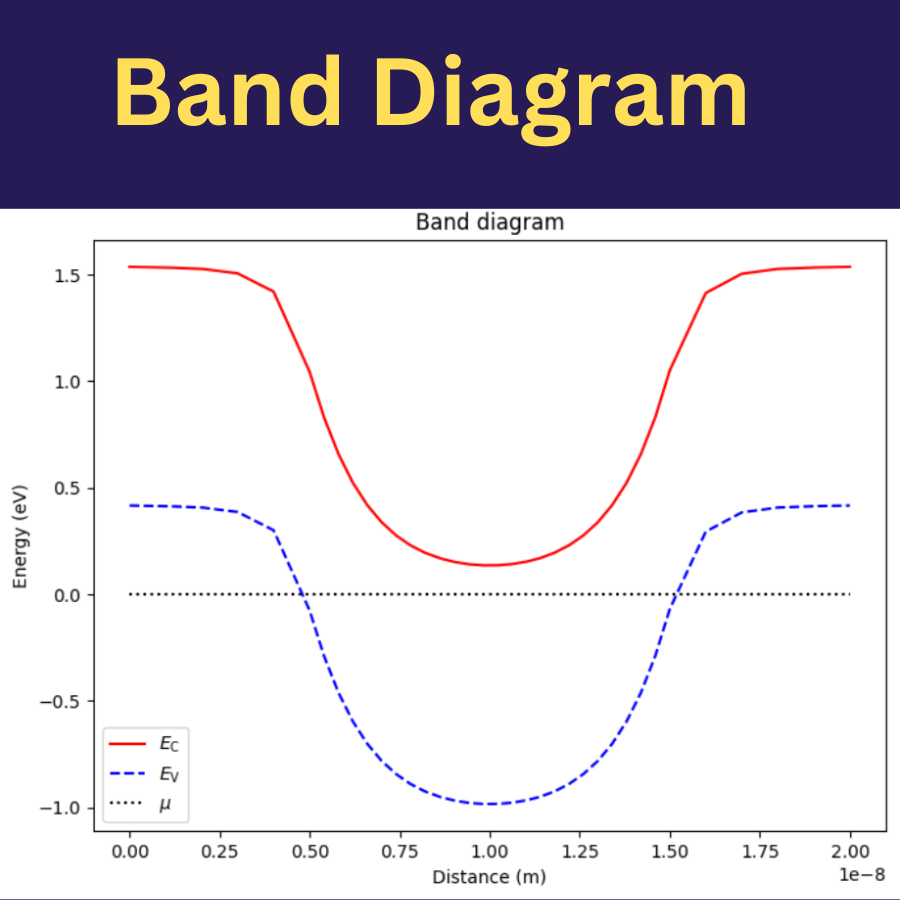
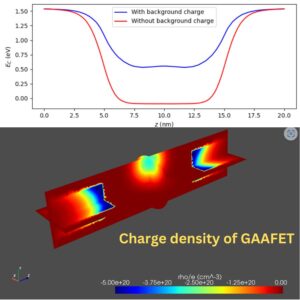
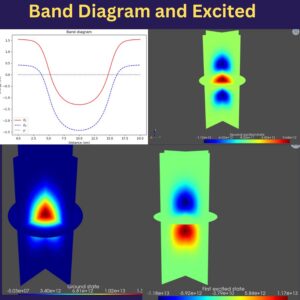
QTCAD’s Schrödinger solver calculates the wave functions of electrons or holes in realistic confinement potentials. These confinement potentials are determined by applying QTCAD’s non-linear Poisson solver to specific device geometries. Thus the computed wavefuntions can be used to predict if a given candidate device can host bound states.

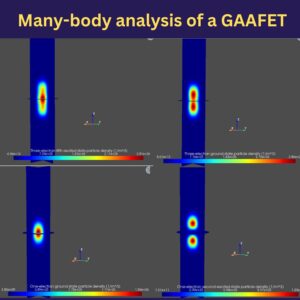
QTCAD can assemble and exactly diagonalize the many-body Hamiltonian for few-electron or few-hole systems under quantum confinement using a truncated basis built from real-space single-body eigenfunctions of the device. This approach yields accurate chemical potentials and addition-energy spectra for realistic quantum dots accounting for the Coulomb interaction between confined electrons or holes.
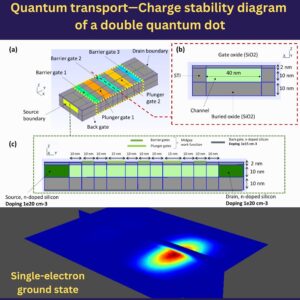
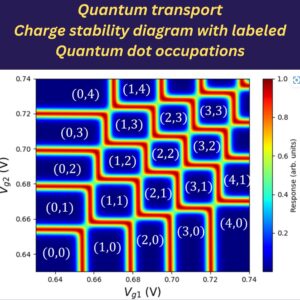
Our master equation solver leverages QTCAD’s many-body physics capabilities to calculate the current flowing through quantum-dot systems in the sequential tunneling regime. This enables the treatment of Coulomb blockade and the prediction of charge stability diagrams used to demonstrate the few-electron or few-hole regime in experiments.
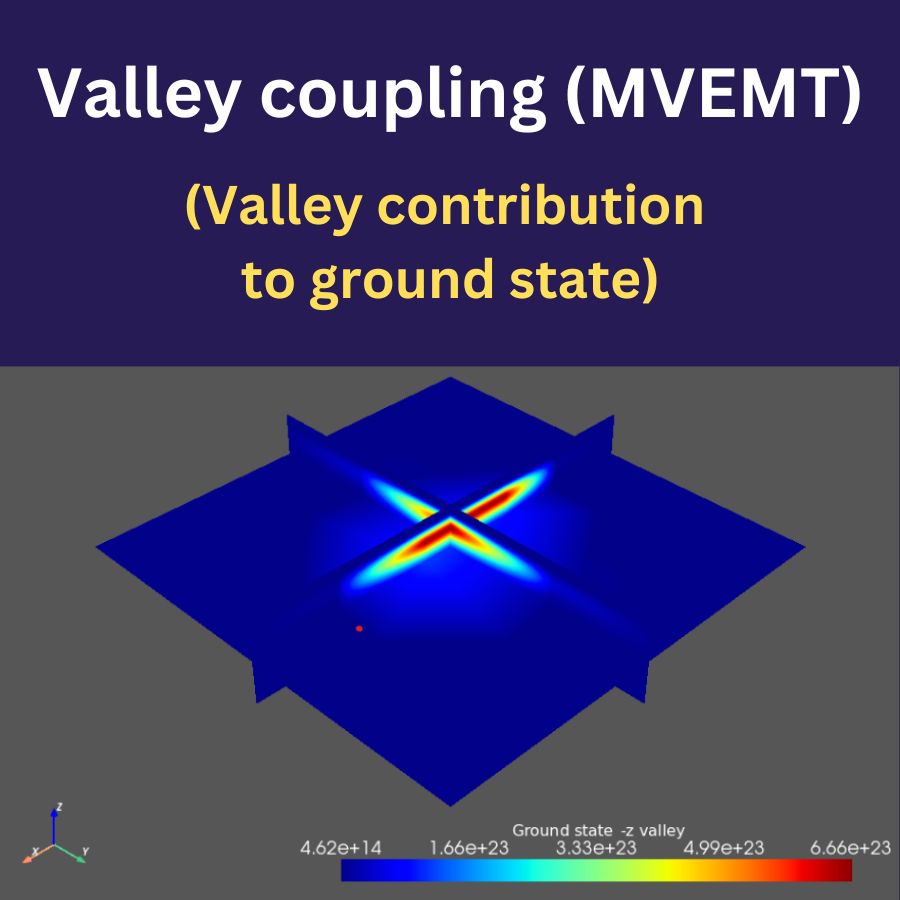
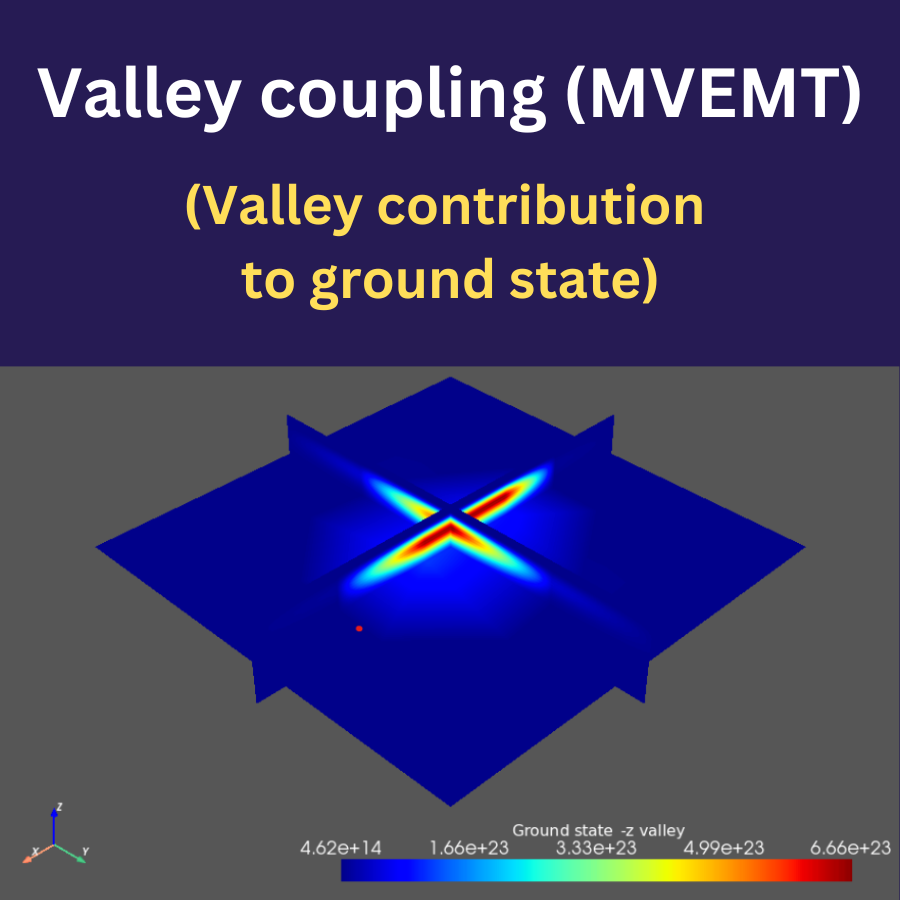
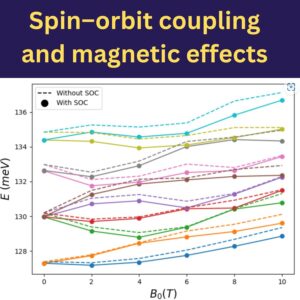
For silicon-based devices, lifting the valley degeneracy is a vital step to isolate well-defined qubit eigenstates. QTCAD includes a module that calculates valley splitting due to sharp heterostructure interfaces using matrix elements in the basis of Bloch states calculated with our atomistic simulation software RESCU.
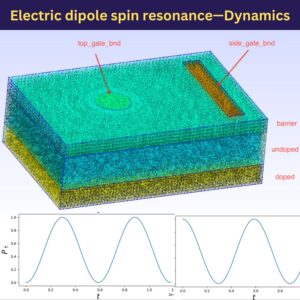
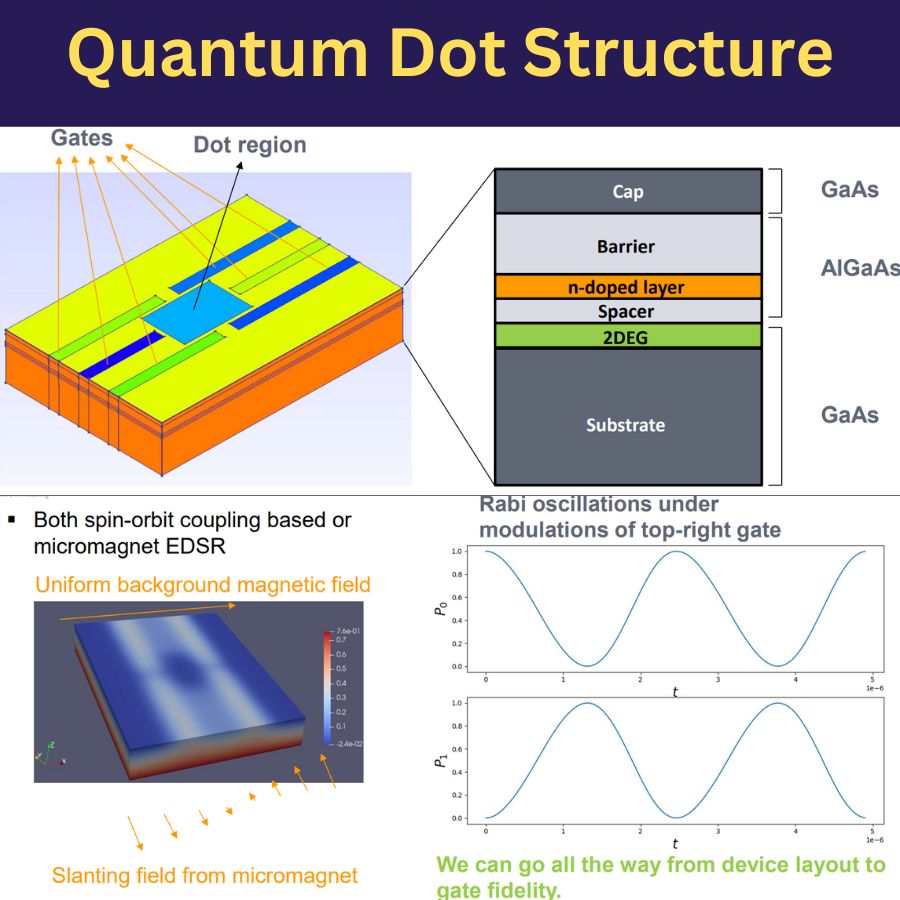
Ultimately, QTCAD determines the system Hamiltonian, accounting for realistic device geometry. Once the system Hamiltonian is known, qubit time-evolution can be evaluated using third-party time-dependent Schrödinger solvers (e.g., QuTiP). In this figure, we show Rabi oscillations for a spin-qubit device under electric-dipole spin resonance. We account for a realistic inhomogeneous magnetic field, and for the precise geometry of electric fields acting on the quantum dot due to applied and charge-noise-induced gate potentials.
In this page, you will learn how to use the three main packages of QTCAD qtcad.device, qtcad.transport, and qtcad.qubit, through below tutorials.